(백준) 4360 – 나무가 아닌 별? (C++)

문제

#4360: 나무가 아니라 별? (acmicpc.net)

번역

루크는 집에 있는 컴퓨터 네트워크를 10MB에서 100MB로 업그레이드하려고 합니다.


하지만 루크가 사용하는 10base2(동축) 케이블은 사용할 수 없습니다.

이는 100Mb 시스템이 100baseT(트위스트 페어) 케이블을 사용하기 때문입니다.


각 100baseT 케이블은 두 개의 장치를 연결할 수 있습니다.

즉, 두 개의 NIC 또는 하나의 NIC와 하나의 허브를 연결할 수 있습니다.

(허브는 여러 케이블을 함께 연결하는 전자 장치입니다.

)

루크는 두 가지 선택이 있습니다.

첫째, 2N-2 네트워크 카드를 구입하여 각 컴퓨터에 넣고 모두 함께 연결할 수 있습니다.


둘째, N개의 네트워크 카드와 허브를 구입하고 N개의 컴퓨터 각각을 허브에 연결할 수 있습니다.


첫 번째 방법은 Luke가 네트워크 트래픽을 전달하도록 운영 체제를 구성해야 함을 의미합니다.

그러나 Winux 2007.2를 설치한 후 네트워크 포워딩이 작동하지 않았습니다.


Luke는 배달 기능을 다시 활성화하는 방법을 몰랐고 Prim이나 Kruskal에 대해 들어본 적이 없었기 때문에 두 번째 방법을 선택했습니다.

즉, N개의 네트워크 카드와 허브를 구입하는 방법입니다.

Luke는 다락방에 살고 있기 때문에 어디에나 케이블을 연결하고 허브를 배치할 수 있습니다.


그러나 컴퓨터는 그것을 움직이지 않을 것입니다.

Luke는 구입해야 하는 케이블의 전체 길이를 최소화하려고 합니다.

첫 번째 입력 줄에는 컴퓨터 수인 양의 정수 N <= 100이 지정됩니다.


N 행이 뒤따르며 각 행은 mm 단위로 공간에서 컴퓨터의 (x,y) 좌표를 제공합니다.

모든 좌표는 0에서 10,000 사이의 정수입니다.


출력은 가장 가까운 mm로 반올림된 케이블 세그먼트의 총 길이를 나타내는 숫자로 구성됩니다.

설명

이는 인공지능에서도 사용되는 ‘경사하강법’을 사용해야 하는 문제다.


결국 Luke는 두 번째 방법을 선택했고 이 경우 케이블 길이를 최소화하는 유일한 방법은 허브를 가능한 한 중앙에 배치하는 것입니다.


이제 케이블에 집중합시다.

모든 점(컴퓨터)을 포함하는 최소 길이 선을 찾아야 합니다.

두 점 사이의 거리를 찾으려면 유클리드 거리($a^{2}+b^{2}=c^{2}$)를 사용해야 하는데 C++의 cmath 헤더 파일에 hypot라는 함수가 있습니다.

. 시도 해봐.

이제 경사하강법을 시도할 차례입니다.


선이 있고 이동하면서 모든 점에 가장 가까운 방향으로 기울기를 변경합니다.


오른쪽 그래프를 보면 경사하강법이 무엇인지 바로 느낄 수 있습니다.

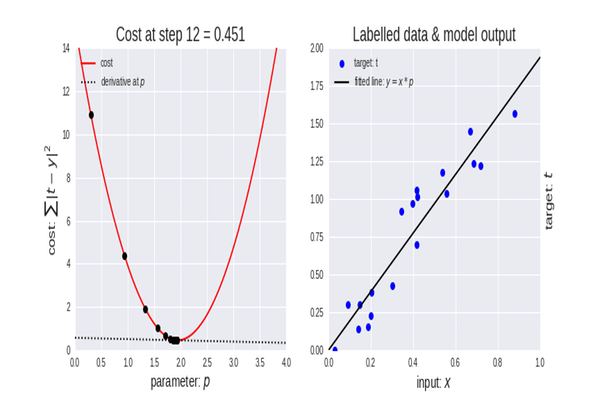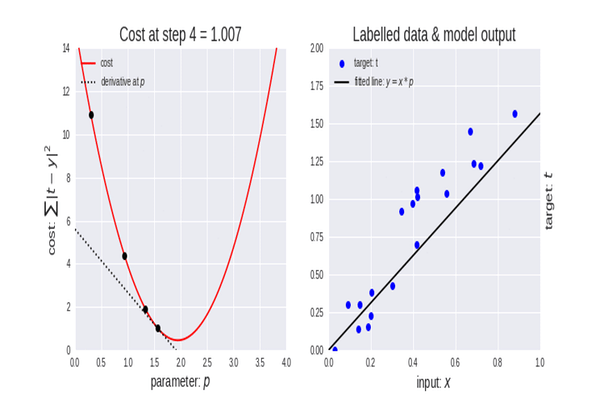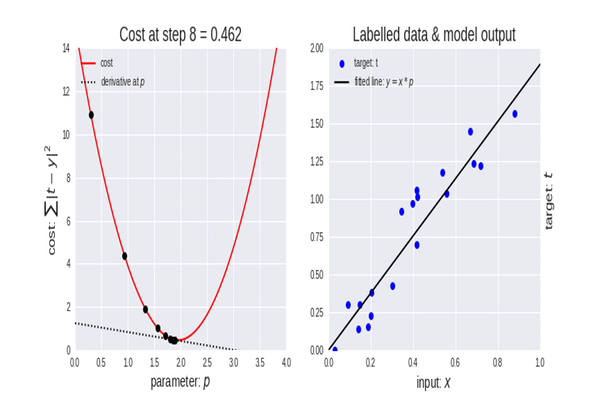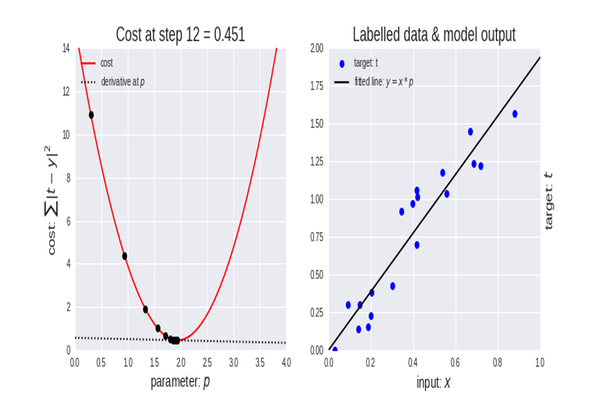
이 코드의 목적은 초기 시작점을 (10000, 10000)으로 설정한 다음 시작점을 이동하면서 sum 함수의 값을 최소화하는 것입니다.


이를 위해 for 문 내에서 i의 값을 점차적으로 감소시켜 시작점을 이동시키고, 이동 후 sum 함수의 값이 이전 값보다 작아지면 해당 위치로 시작점을 이동시킨다.


마지막으로 round 함수를 사용하여 최종 경로의 길이를 정수로 반환합니다.

#include <iostream>
#include <cmath>
using namespace std;

int N;
int x(100), y(100);

double sum(double a, double b) {
   double result = 0;
   for (int i = 0; i < N; i++) {
      result += hypot(x(i) - a, y(i) - b);
   }
   return result;
}

int main() {
   cin >> N;
   for (int i = 0; i < N; i++) {
       cin >> x(i) >> y(i);
   }
   
   int a = 10000;
   int b = 10000;
   
   for (int i = 10000; i > 0.0001; i *= 0.9) {
       if (sum(a + i, b) < sum(a, b)) {
           a += i;
       }
       if (sum(a - i, b) < sum(a, b)) {
           a -= i;
       }
       if (sum(a, b + i) < sum(a, b)) {
           b += i;
       }
       if (sum(a, b - i) < sum(a ,b)) {
           b -= i;
       }
   }
   
   cout << round(sum(a, b));
   
   return 0;
}